使用优秀的主题,本文将不会引起恐慌。希望未来能实现查看版本控制,类似wiki的编辑历史。
day0
与去年不同的是,今年的day0上午讲了去年的题目和搜索,并没有信心赛;实际上,这次基本上没有信心赛。运动会在十一之后就开了,回去就是期中考。
我们在13:00出发,比较准确的用了一个半小时到达了旅馆,房卡也很快拿到了,体验比以前好多了。不同的是,现在身份证还要人脸识别一下,但还是很快的。旅馆看起来还是不错的。

接着又乘车前往学军中学,但得去绕一圈,以及学校里面和外面似乎都有围墙。袋子看起来很好,而餐券更加神奇,看起来就像门票一样。少数人需要去实验楼比赛,大部分都在体育馆。小卖部、宿舍看起来都很厉害的样子,然而晚饭改变了我们的想法。







没到规定的五点就能吃饭了,需要排队,拿一个托盘,就像快餐一样。正当我思考能拿几个菜的时候,突然发现一共就只有三个菜……所有人都拿了同样的三个菜,以及橘子和空碗,要再排队去盛饭和汤。餐券也没留下,整张被收走了。处理更奇葩,需要拿到盛饭的地方,把所有的菜(饭?)倒掉,然后放到一个传送带上,送到里面,由人工分拣……
今年没有了fks,晚上比较寂寞,我连小说也没看,认真的在看模板。顺便推销了一下我暑假就开始改写的TNPQ,这个基本完成之后我会放出beta版让大家试用的。
day1
早上自助餐,总体来讲还是不错的。我一直以为是8点开始,其实是8:30,所以我们在门口等了一会儿。大家都在聊Tarjan,我又不太记得这些了,大概问了一下。少数几个可能是因为初赛卡线在机房比赛,剩下的都在体育馆二楼。整个体育馆都是电脑,真有NOI的气势,其实我也没去过NOI现场。不过都是笔记本。
坐下来不能动笔记本。等到开始之后,我先看了一下,居然有vscode!当然emacs和gvim照例也是有的。不过我显然没有心思去配code,当然还是按原计划用dev。OS还是Windows 7。
更令人惊讶的是,评测机居然变成Intel® Core™ i7-8700K CPU @ 3.70GHz,内存32GB!很多人都到最后才发现这一点,这可能是报名费涨价的原因。
铺设道路(road)
题意
给定长度为$n$的序列,每次可以选择一个区间$l\dots r$,满足区间内都大于0,将整个区间都减1。求最少的操作次数,使序列全为0。
数据范围
- 对于30%的数据,$n\le 10$。
- 对于70%的数据,$n\le 1000$。
- 对于100%的数据,$n\le 100,000$。
思路
并没有太好的思路,看起来可以模拟。显然对于每个区间都操作区间内最小值次,然后把区间按照最小值的位置分成左右两半,继续操作。这可以用线段树维护,当然ST表也可以,复杂度$\mathcal O(n\log n)$。当然我相信有更简单的做法,毕竟这是D1T1,但不管了。
尝试发现dfs可能会爆栈,果断改成bfs。
road.cpp1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| #include<fstream>
#include<algorithm>
using namespace std;
ifstream fin("road.in");
ofstream fout("road.out");
const int N=100005;
int n,a[N];
pair<int,int> tree[N*4];
long long ans;
struct state
{
int l,r,now;
}q[N];
void build(int id,int l,int r)
{
if(l==r)
tree[id]=make_pair(a[l],l);
else
{
int mid=(l+r)/2;
build(id*2,l,mid);
build(id*2+1,mid+1,r);
tree[id]=min(tree[id*2],tree[id*2+1]);
}
}
pair<int,int> query(int id,int l,int r,int L,int R)
{
if(L<=l&&R>=r)
return tree[id];
int mid=(l+r)/2;
if(R<=mid)
return query(id*2,l,mid,L,R);
if(L>mid)
return query(id*2+1,mid+1,r,L,R);
return min(query(id*2,l,mid,L,R),query(id*2+1,mid+1,r,L,R));
}
int main()
{
fin>>n;
for(int i=1;i<=n;i++)
fin>>a[i];
build(1,1,n);
int l=1,r=1;
q[1].l=1;q[1].r=n;q[1].now=0;
for(;l<=r;l++)
{
pair<int,int> mn=query(1,1,n,q[l].l,q[l].r);
ans+=mn.first-q[l].now;
if(mn.second>q[l].l)
{
q[++r].l=q[l].l;q[r].r=mn.second-1;q[r].now=mn.first;
}
if(mn.second<q[l].r)
{
q[++r].l=mn.second+1;q[r].r=q[l].r;q[r].now=mn.first;
}
}
fout<<ans<<endl;
return 0;
}
|
貌似是NOIp2013原题……

货币系统(money)
题意
有$n$种货币,每种面额已知且都有无限张,求与其等价的货币系统的货币种数的最小值。等价指一个数要么两个系统都能表示,要么都不能表示。
数据范围
比较复杂,偷懒直接用洛谷的图了。
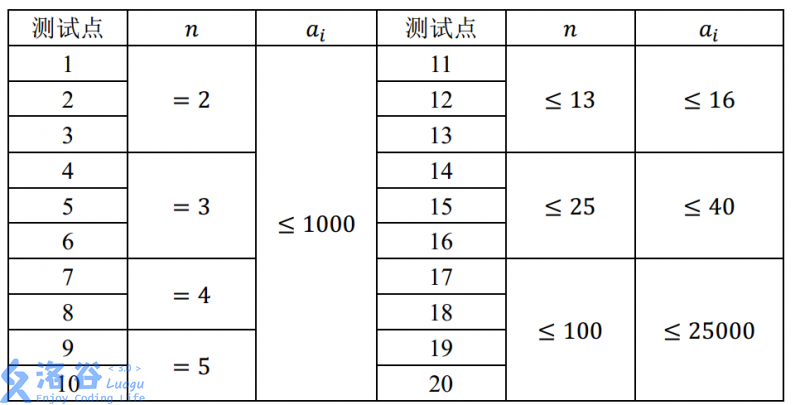
思路
感觉是个数学题,特别不可做。看了一下大样例,才发现等价的一定是原来的子集,只要能被其他数表示的数都可以删掉,这样就是个完全背包了。考虑对面额排序,从大到小,用还没删掉的货币表示当前面额,如果可以就删掉,否则保留。这样的复杂度是$\mathcal O(Tn^2m)$的,过不去。线段树优化背包?$\mathcal O(Tn\log nm)$,看起来还是很悬,而且很难写。bitset优化?貌似只有01背包可以。于是弃疗开T3。
money.cpp1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| #include<fstream>
#include<algorithm>
using namespace std;
ifstream fin("money.in");
ofstream fout("money.out");
const int N=105,M=25005;
int a[N];
bool f[M],del[N];
int main()
{
int t;
fin>>t;
while(t--)
{
int n;
fin>>n;
for(int i=1;i<=n;i++)
fin>>a[i];
sort(a+1,a+n+1);
fill(del+1,del+n+1,false);
for(int i=n;i;i--)
{
fill(f+1,f+a[i]+1,false);
f[0]=true;
for(int j=1;j<=n;j++)
if(j!=i&&!del[j])
for(int k=a[j];k<=a[i];k++)
f[k]|=f[k-a[j]];
del[i]=f[a[i]];
}
fout<<count(del+1,del+n+1,false)<<endl;
}
return 0;
}
|
似乎只要从小到大处理就可以去掉那个该死的$n$了……不过民间数据我都过了,然而官方数据还是卡掉了。
赛道修建(track)
题意
给定一棵有边权的树,选出$m$条不相交的路径,使长度最短的路径长度最长。
数据范围
继续搬洛谷。
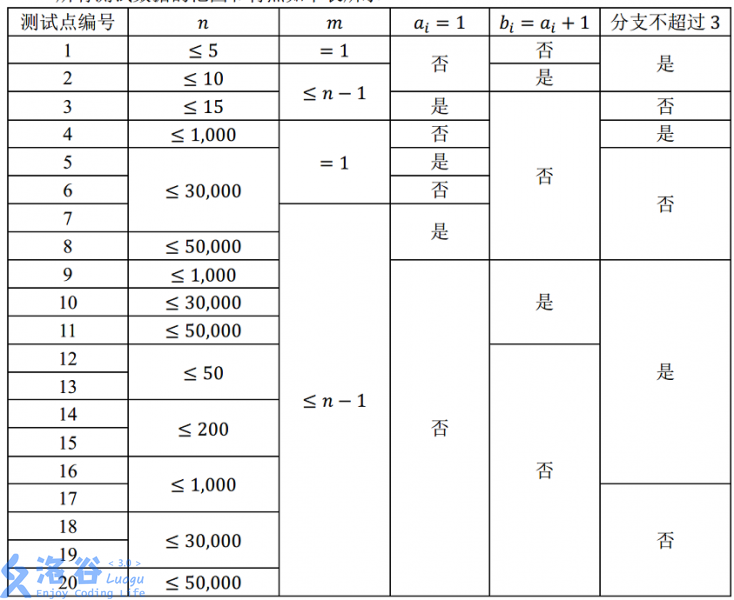
思路
部分分很丰富。$m=1$就是求直径。否则显然二分,链和菊花树随便贪心。这样55分。然后我就不会了。我能想到的多项式算法是把所有路径提出,做一遍最大独立集,但好像$n=50$都过不了。
11点多发现菊花树写错了,要改成multiset贪心。
track.cpp1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
| #include<fstream>
#include<algorithm>
#include<cstdlib>
#include<set>
using namespace std;
ifstream fin("track.in");
ofstream fout("track.out");
const int N=50005;
int n,m,head[N],v[N*2],w[N*2],nxt[N*2],id[N*2],e;
inline void add_edge(int u,int v,int w,int id)
{
::v[++e]=v;
::w[e]=w;
::id[e]=id;
nxt[e]=head[u];
head[u]=e;
}
int f[N],g[N],ans,chain[N],len[1005][1005],p[1005*1005];
pair<int,int> np[1005*1005];
void dfs(int u,int fat)
{
for(int i=head[u];i;i=nxt[i])
if(v[i]!=fat)
{
dfs(v[i],u);
if(f[v[i]]+w[i]>=f[u])
{
g[u]=f[u];
f[u]=f[v[i]]+w[i];
}
else if(f[v[i]]+w[i]>g[u])
g[u]=f[v[i]]+w[i];
}
ans=max(ans,f[u]+g[u]);
}
bool f1,f2;
unsigned now[32],path[1005][1005][32];
bool check(int mid)
{
if(f1)
{
int cnt=0;
multiset<int> S;
for(int i=n-1;i;i--)
if(w[i]>=mid)
cnt++;
else
S.insert(w[i]);
while(S.size()>=2)
{
int mx=*S.rbegin();
S.erase(--S.end());
set<int>::iterator it=S.lower_bound(mid-mx);
if(it==S.end())
break;
cnt++;
S.erase(it);
}
return cnt>=m;
}
if(f2)
{
int cnt=0,sum=0;
for(int i=1;i<n;i++)
{
sum+=chain[i];
if(sum>=mid)
{
cnt++;
sum=0;
}
}
return cnt>=m;
}
int cc=0;
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
if(len[i][j]>=mid)
np[++cc]=make_pair(i,j);
int ans=0;
for(int t=1;1ll*t*n*n*n/32<=2e6;t++)
{
for(int i=1;i<=cc;i++)
p[i]=i;
random_shuffle(p+1,p+cc+1);
for(int i=0;i<=n/32;i++)
now[i]=0;
int cnt=0;
for(int i=1;i<=cc;i++)
{
bool flag=true;
for(int j=0;j<=n/32;j++)
if(path[np[p[i]].first][np[p[i]].second][j]&now[j])
{
flag=false;
break;
}
if(flag)
{
cnt++;
for(int j=0;j<=n/32;j++)
now[j]|=path[np[p[i]].first][np[p[i]].second][j];
}
ans=max(ans,cnt);
}
}
return ans>=m;
}
void dfs2(int u,int fat,int dist,int rt)
{
for(int i=0;i<=n/32;i++)
path[rt][u][i]=now[i];
len[rt][u]=dist;
for(int i=head[u];i;i=nxt[i])
if(v[i]!=fat)
{
now[id[i]/32]^=1<<(id[i]&31);
dfs2(v[i],u,dist+w[i],rt);
now[id[i]/32]^=1<<(id[i]&31);
}
}
int main()
{
srand(1e9+7);
fin>>n>>m;
f1=f2=true;
int sum=0;
for(int i=1;i<n;i++)
{
int u,v,w;
fin>>u>>v>>w;
sum+=w;
if(u!=1)
f1=false;
if(v!=u+1)
f2=false;
add_edge(u,v,w,i);
add_edge(v,u,w,i);
}
if(m==1)
{
dfs(1,0);
fout<<ans<<endl;
return 0;
}
if(f1)
{
for(int i=1;i<n;i++)
w[i]=w[i*2];
sort(w+1,w+n);
}
if(f2)
{
int cc=0;
for(int i=1;i<n;i++)
for(int j=head[i];j;j=nxt[j])
if(v[j]==i+1)
chain[++cc]=w[j];
}
if(!f1&&!f2)
for(int i=1;i<=n;i++)
dfs2(i,0,0,i);
int l=0,r=sum/m,ans=0;
while(l<=r)
{
int mid=(l+r)/2;
if(check(mid))
{
l=mid+1;
ans=mid;
}
else
r=mid-1;
}
fout<<ans<<endl;
return 0;
}
|
真送命题。作业里有原题CF1042F Leaf Sets,很多人都A了这题,直接贪心即可。我怎么就没想到呢?不过也有细节问题,比如swwind用了set而不是multiset,fks方向不对。
剩下的时间
一堆人AK,感觉没救了。下午看了很长时间的BlogClan,主要看了关于猫毛色基因的文章,还在维基上看了规范的版本。晚饭没去学校吃,而是在swwind和lzq的房间里一起点了外卖。看了一会儿新书Crowfeather’s Trial。
不能像去年那样看《自然传奇》了,它改名为《自然》,而且最近都在放我早就看过的纪录片Africa。
day2
去学军的路上,sigma说day2可能很难,因为day1太简单了。我感到不妙。
旅行(travel)
题意
给定一棵树或环套树,求字典序最小的dfs序。
数据范围
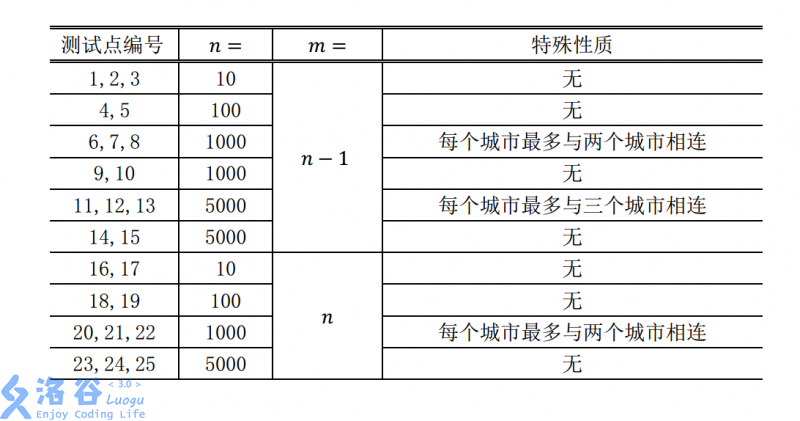
思路
树显然以1为根,把出边排序dfs即可。环套树就比较麻烦,好像可以贪心,确定1的位置在树上还是环上,但很难写。所幸$n\le 5,000$,观察样例发现环上显然有一条边不会经过,直接在环上断边,再dfs,找到最小的方案即可。至于找环,最近做了不少类似的题,比较熟练的写出来了。
排序当然可以预处理,复杂度$\mathcal O(n^2)$。vector会不会被卡常?如果改成边表,就要取出来排序,再开一个新的边表,太麻烦了。想到评测机,我决定不改了。
travel.cpp1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
| #include<fstream>
#include<algorithm>
#include<vector>
using namespace std;
ifstream fin("travel.in");
ofstream fout("travel.out");
const int N=5005;
vector<int> mat[N];
int n,m,ans[N],cc,s[N],sp,cycle[N],cp,du,dv,Ans[N];
void dfs(int u,int fat)
{
ans[++cc]=u;
for(int i=0;i<mat[u].size();i++)
if(mat[u][i]!=fat&&!((du==u&&dv==mat[u][i])||(du==mat[u][i]&&dv==u)))
dfs(mat[u][i],u);
}
bool ins[N],vis[N];
void find_cycle(int u,int fat)
{
s[++sp]=u;
ins[u]=true;
vis[u]=true;
for(int i=0;i<mat[u].size();i++)
if(mat[u][i]!=fat)
{
if(!ins[mat[u][i]])
{
if(!vis[mat[u][i]])
find_cycle(mat[u][i],u);
}
else
{
for(;s[sp]!=mat[u][i];sp--)
cycle[++cp]=s[sp];
cycle[++cp]=mat[u][i];
}
}
ins[u]=false;
if(s[sp]==u)
sp--;
}
void cut()
{
cc=0;
dfs(1,0);
for(int i=1;i<=n;i++)
if(ans[i]<Ans[i])
break;
else if(ans[i]>Ans[i])
return;
copy(ans+1,ans+n+1,Ans+1);
}
int main()
{
fin>>n>>m;
for(int i=1;i<=m;i++)
{
int u,v;
fin>>u>>v;
mat[u].push_back(v);
mat[v].push_back(u);
}
for(int i=1;i<=n;i++)
sort(mat[i].begin(),mat[i].end());
if(m==n-1)
{
dfs(1,0);
for(int i=1;i<=n;i++)
fout<<ans[i]<<' ';
fout<<endl;
}
else
{
find_cycle(1,0);
Ans[1]=n;
for(int i=1;i<cp;i++)
{
du=cycle[i];dv=cycle[i+1];
cut();
}
du=cycle[cp];dv=cycle[1];
cut();
for(int i=1;i<=n;i++)
fout<<Ans[i]<<' ';
fout<<endl;
}
return 0;
}
|
$\mathcal O(n)$贪心确实是可做的,然而并没有必要。有些人在dfs里面sort,$\mathcal O(n^2\log n)$,完美卡常。
填数游戏(game)
题意
将$n\times m$的矩阵填上01,对于一个从左上走到右下的方案$P$,用D/R表示走的方向,可以得到一个走法字符串$w§$和一个数字字符串$s§$。一个矩阵合法,仅当任意两条路径$P_1,P_2$,如果$w(P_1)>w(P_2)$,那么必须满足$s(P_1)\le s(P_2)$。求合法的矩阵数。
数据范围
| 测试点 |
$n\le$ |
$m\le$ |
| 1~4 |
3 |
3 |
| 5~10 |
2 |
1,000,000 |
| 11~13 |
3 |
1,000,000 |
| 14~16 |
8 |
8 |
| 17~20 |
8 |
1,000,000 |
思路
假题吧?毫无思路。打了爆搜,然后考虑矩阵优化状压,状压最后一列的数。看起来很有道理,但答案就是错的。不过$n=2$时是对的。$n=3$我怎么也搞不对。
game.cpp1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
| #include<fstream>
#include<algorithm>
using namespace std;
ifstream fin("game.in");
ofstream fout("game.out");
const int N=8,M=1000005,MOD=1e9+7;
int n,m,f[M][1<<3];
namespace bf
{
int ans,cc,W[M],P[M],cnt;
bool board[N][N],now,vis[1<<N][1<<N];
void walk(int x,int y,int w,int p)
{
if(x==n&&y==m)
{
for(int i=1;i<=cc;i++)
if((w>W[i]&&p>P[i])||(w<W[i]&&p<P[i]))
{
now=false;
return;
}
W[++cc]=w;
P[cc]=p;
return;
}
if(x<n)
walk(x+1,y,w*2,p*2+board[x+1][y]);
if(y<m)
walk(x,y+1,w*2+1,p*2+board[x][y+1]);
}
void dfs(int x,int y)
{
if(x==n+1)
{
now=1;
cc=0;
walk(1,1,0,board[1][1]);
ans+=now;
if(now)
{
int pred=0,now=0;
for(int i=1;i<=n;i++)
{
pred=pred*2+board[i][m-1];
now=now*2+board[i][m];
}
vis[pred][now]++;
}
}
else
{
board[x][y]=0;
if(y<m)
dfs(x,y+1);
else
dfs(x+1,1);
board[x][y]=1;
if(y<m)
dfs(x,y+1);
else
dfs(x+1,1);
}
}
};
int main()
{
fin>>n>>m;
if(n<=3&&m<=3)
{
bf::dfs(1,1);
fout<<bf::ans<<endl;
}
else if(n<=2)
{
int t=m;
m=n;
bf::dfs(1,1);
m=t;
for(int i=0;i<1<<n;i++)
f[1][i]=1;
for(int i=2;i<=m;i++)
for(int j=0;j<1<<n;j++)
for(int k=0;k<1<<n;k++)
{
if(bf::vis[k][j])
f[i][j]=(f[i][j]+f[i-1][k])%MOD;
}
int ans=0;
for(int i=0;i<1<<n;i++)
ans=(ans+f[m][i])%MOD;
fout<<ans<<endl;
}
else
{
bf::dfs(1,1);
fout<<bf::ans<<endl;
}
return 0;
}
|
打表找规律!我怎么又忘了。事实上$m>n$时是很有规律的,这样很多人拿了65甚至更多。不过$n=8$是很难搜出来的。
保卫王国(defense)
题意
给定一棵有点权的树,要求选一些点,满足每条边两端至少选了一个点。每次询问规定2个点必须选/不选,求最小代价。无解输出-1。
数据范围
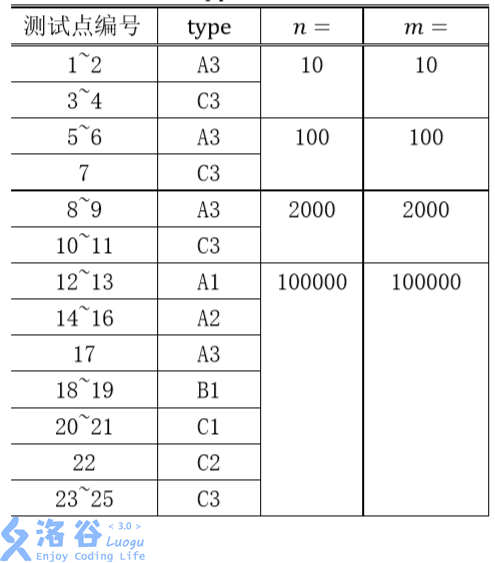
数据类型的含义:
- A:树为一条链。
- B:树深不超过100。
- C:树形态无特殊约束。
- 1:询问时保证要求选择1号点。
- 2:询问时保证两个点相邻。
- 3:询问无特殊约束。
思路
$\mathcal O(n^2)$暴力随便树形DP一下。想了一会儿,并没想到链的做法。
为什么是defense而不是defence?
defense.cpp1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
| #include<fstream>
#include<string>
#include<algorithm>
using namespace std;
ifstream fin("defense.in");
ofstream fout("defense.out");
const int N=100005,INF=1e9;
int p[N],head[N],v[N*2],nxt[N*2],e,a,x,b,y,dp[N][2];
inline void add_edge(int u,int v)
{
::v[++e]=v;
nxt[e]=head[u];
head[u]=e;
}
void dfs(int u,int fat)
{
dp[u][0]=dp[u][1]=INF;
if(a==u)
{
if(x)
dp[u][1]=p[u];
else
dp[u][0]=0;
}
else if(b==u)
{
if(y)
dp[u][1]=p[u];
else
dp[u][0]=0;
}
else
{
dp[u][1]=p[u];
dp[u][0]=0;
}
for(int i=head[u];i;i=nxt[i])
if(v[i]!=fat)
{
dfs(v[i],u);
if(dp[v[i]][1]!=INF&&dp[u][0]!=INF)
dp[u][0]+=dp[v[i]][1];
else
dp[u][0]=INF;
if(min(dp[v[i]][0],dp[v[i]][1])!=INF&&dp[u][1]!=INF)
dp[u][1]+=min(dp[v[i]][0],dp[v[i]][1]);
else
dp[u][1]=INF;
}
}
int main()
{
int n,m;
string type;
fin>>n>>m>>type;
for(int i=1;i<=n;i++)
fin>>p[i];
for(int i=1;i<n;i++)
{
int u,v;
fin>>u>>v;
add_edge(u,v);
add_edge(v,u);
}
while(m--)
{
fin>>a>>x>>b>>y;
dfs(1,0);
int ans=INF;
if(a==1)
ans=dp[1][x];
else if(b==1)
ans=dp[1][y];
else
ans=min(dp[1][0],dp[1][1]);
if(ans==INF)
fout<<-1<<'\n';
else
fout<<ans<<'\n';
}
return 0;
}
|
貌似B性质很容易写。另外这题还是DDP(动态动态规划?)的模板题。
几天之后

| road |
money |
track |
travel |
game |
defense |
总分 |
| 100 |
80 |
55 |
100 |
50 |
44 |
429 |
还是去年分数高……今年难度有点难说,不过确实暴露了很多问题。我不太可能能去PKUWC之类的,所以基本AFO。
洛谷最近推出了咕值排名,我已经从200+掉到了300+名。我很奇怪为什么我日报投稿没能加贡献。















