学习光线追踪
本文为 xlab 学习笔记,打算包含光线追踪与光栅化的差异、Whitted 风格光线追踪(Witted!)、BVH 加速等,如果有可能还想了解一下实时光线追踪的硬件加速(RTX!)以及路径追踪。
图形学初学者(暑假才开始学),如有错误欢迎指正。
前言
为什么选择光线追踪呢?一方面 RTX 使得其确实在这几年比较火,另一方面在今年 CPC 决赛题目就是优化 Blender Cycles 的渲染,其实就是光线(路径)追踪,虽然我们最近一直都在做降噪(denoise)。另外「汇编与接口」下一次 SIMD 实验我也打算优化朴素的光线追踪实现。
P.S. CPC 无了,我们到最后还是没优化光追,降噪也一言难尽
可能需要读者有一定的图形学基础。如果没有可以简单学一学 GAMES101,非常推荐。至少可以过一下课件,如果有时间可以看 B 站课程视频。
本文基本上就是根据 GAMES101 光线追踪(基本原理、加速结构)的逻辑写的,后面的两讲就是路径追踪的高级内容,比较困难,不一定会写。大部分图片来自 GAMES101 课件,否则会标明来源。
对于来自 xlab 的读者:本文将会不断更新,最终会放到 wiki 上的,现在暂时先放链接。
我校的图形学课程也可以看看,我现在就在学,不过现在还没讲到着色和光线追踪。
简介
计算机图形学渲染通常可以分为实时渲染与离线渲染,实时渲染通常用在游戏中,离线渲染通常用在动画、特效等。实时渲染的渲染速度要求很高,因此通常使用光栅化(Rasterization)来渲染,而离线渲染则可以使用质量更好的光线追踪(Ray Tracing)来渲染。
- 光栅化
- 将场景中的物体投影到屏幕上,然后对每个像素进行着色。相当于是光源发出的光经过物体反射,直接进入了摄像机,就是直接光照。
- 优点:渲染速度快。
- 缺点:无法实现间接光照、全局光照、折射、折射等效果。
- 以下是经典的 Blinn-Phong 模型:

Blinn-Phong
- 光线追踪
- 从每个像素发出一条光线,然后计算光线与场景中物体的交点,然后计算交点的着色,并可以继续这个过程,直到光线消失或者达到最大追踪深度。
- 优点:可以实现更真实的光照效果。
- 缺点:计算量大,渲染速度慢。
- 以下是经典的 Whitted 模型:
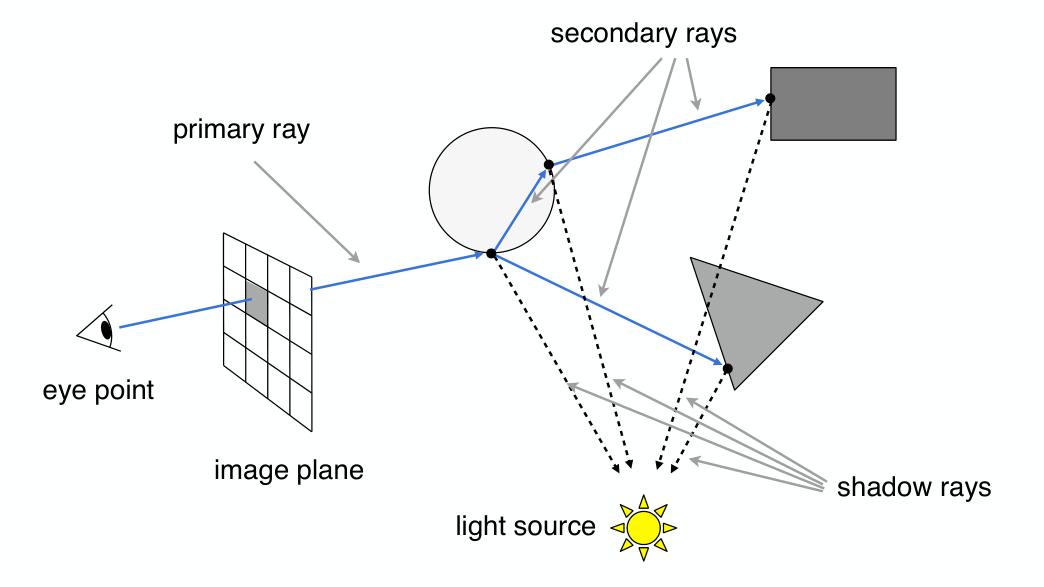
Whitted
- 路径追踪:综合光线追踪等多种技术,使用 Monte Carlo 方法来进行光线追踪,可以实现更真实的光照效果。
我的理解是,一般说光线追踪,指的可能是 Whitted 风格这样的简单版本,也可能就是指路径追踪。
下图比较了光栅化、光线追踪、路径追踪的渲染效果(来源 NVIDIA 博客):

想感受一下光线追踪的渲染过程?可以找个复杂的模型(最好是 PBR?)让 Blender 渲染看看(
Whitted 风格光线追踪
基本原理
光沿直线传播,而且具有光路可逆性。正常情况下,光源发出一条光线,光线经过物体多次反射、折射,最终到达摄像机。然而,如果从光源向随机方向发出的光线,不太可能会到达摄像机,这样直接模拟的效率就很低。
因此,我们可以从摄像机发出「观察线」,其性质与光线完全相同,只是方向相反。当「观察线」与物体相交时,计算其与各个光源之间是否有遮挡,如果没有遮挡,则计算交点的着色,作为该像素的颜色。
这种方法称为「ray casting」,如下图所示:
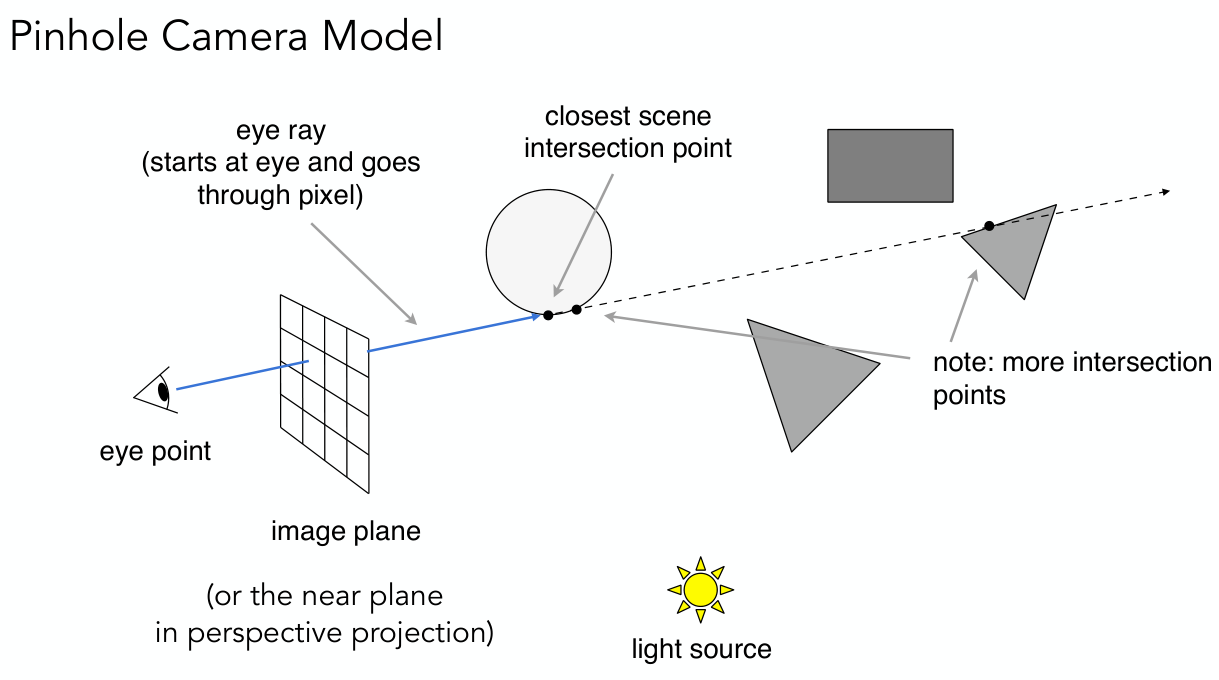
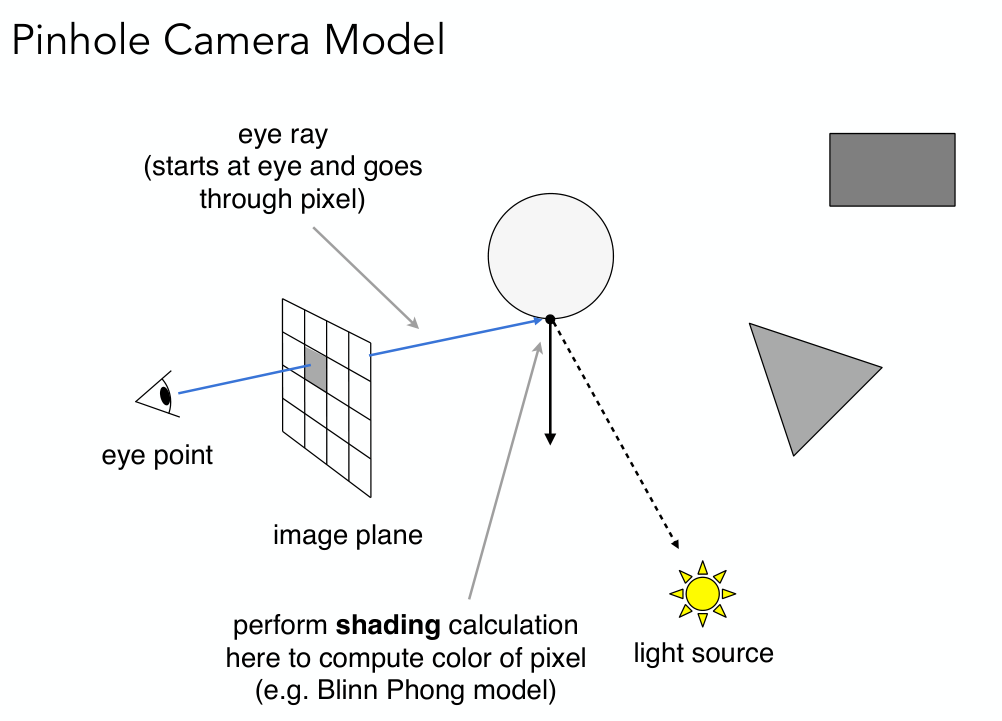
「观察线」的方向就是摄像机与(透视投影)近平面上某个像素的连线,这样就可以计算出每个像素的颜色。也就是说,每个像素都需要发出一条「观察线」。
递归追踪
上面的示意图只展示了一次反射的情况,和直接着色差不多。实际上光线追踪当然可以实现多次反射、折射等效果,只需要在计算交点的着色时,再发出一条「观察线」,然后递归地计算交点的着色即可。

如图,「观察线」在球体上一分为二,分别进行了镜面反射和折射,然后再继续传播。可以注意到,除了从矩形到光源的连线被三角形遮挡外,其他的光线都没有遮挡,因此都需要参与着色计算。
另外,根据能量守恒,光线的总能量是不会超出初始值的,但可能发生能量损失,因此需要对能量进行衰减。
效果
下图是 Whitted 风格光线追踪的效果:

这就是当时 Whitted 用来展示光线追踪的图像,可以看到,折射、反射效果都很好,但是光线追踪的效率很低,因为每个像素都需要发出一条「观察线」。在当时的 VAX 11/780 上需要 74 分钟才能渲染出这张图。但在现代 GPU 上,完全可以实时渲染出这张图。
数学表示
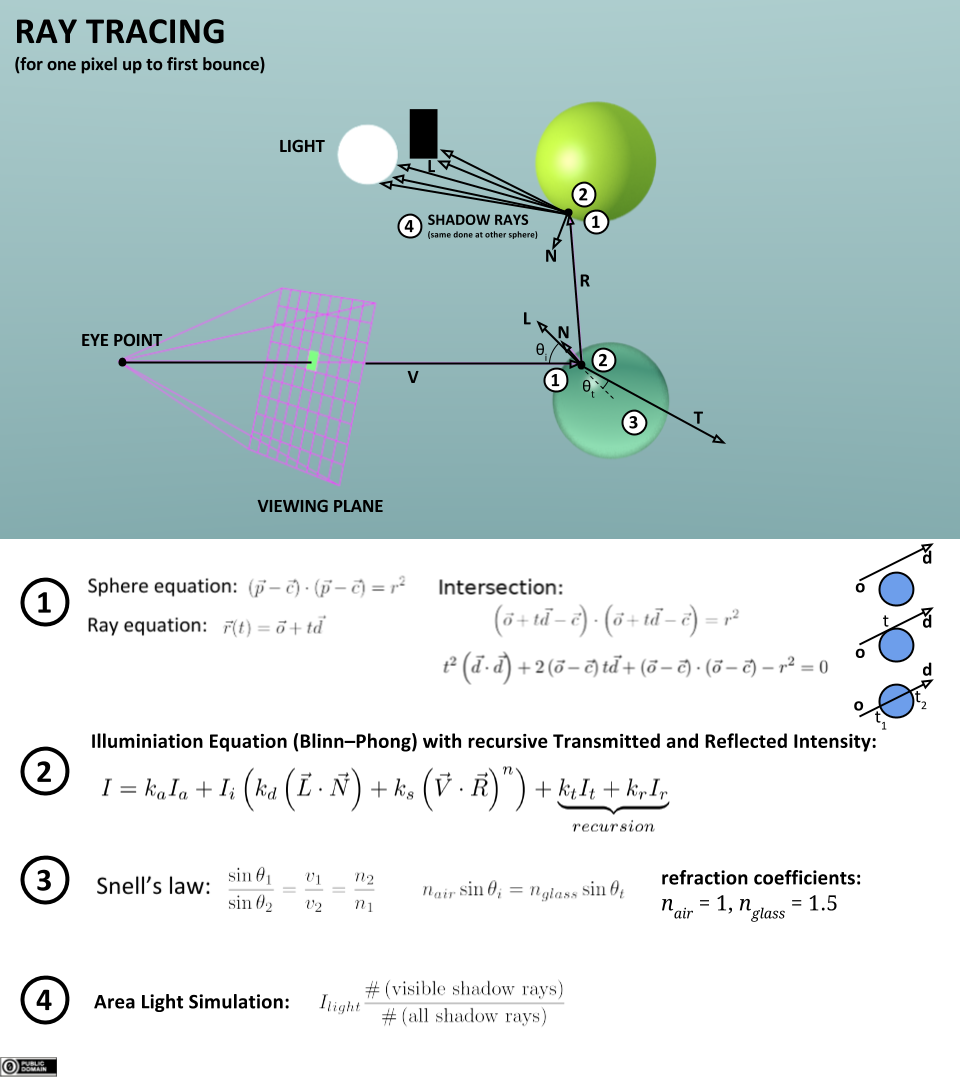
来源:Wikipedia
光线
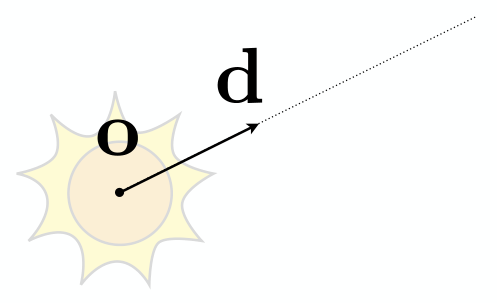
光线可以用射线来表示,由原点和方向向量组成。我们还引入参数 t,用来表示光线上的点。因此光线可以表示为
$$\textbf{r}(t) = \textbf{o} + t\textbf{d} \qquad (t \ge 0)$$
与隐曲面相交的点可以表示为
$$\textbf{p} = \textbf{r}(t)$$
其中,隐曲面的方程为
$$f(\textbf{p}) = 0$$
这样就可以求解出 t,从而得到交点。
平面
我们规定平面方程为
$$(\textbf{p}-\textbf{p}_0)\cdot\textbf{n} = 0$$
其中,$\textbf{p}_0$ 是平面上的一点,$\textbf{n}$ 是平面的法向量。我们可以用这个方程来判断光线与平面的关系,如果光线与平面相交,那么光线上就存在点满足上面的方程。
光线与三角形相交
在实际的应用中,很少用到参数曲面或隐曲面,一般(尤其是游戏中)都用三角形(多边形)网格来表示物体。因此,我们更关心光线与三角形(平面)相交的问题。
显然,光线所在的直线和三角形所在的平面除了平行就是相交,在实际中基本不可能是平行的。但要和三角形相交,交点就必须在三角形内,而且必须在光线的正方向上($t \ge 0$)。
联立光线和平面方程,可以得到
$$t = \frac{(\textbf{p}_0-\textbf{o})\cdot\textbf{n}}{\textbf{d}\cdot\textbf{n}} \qquad (t \ge 0)$$
判断交点是否在三角形内,比较容易想到的方法是计算交点与任意两点组成的三个三角形面积和是否等于原三角形面积。计算三角形面积可以用叉积。不过,计算量更小的方法是使用重心坐标。重心坐标的定义是
$$\textbf{p} = \alpha\textbf{p}_1 + \beta\textbf{p}_2 + \gamma\textbf{p}_3$$
其中,$\alpha + \beta + \gamma = 1$。我们可以用这个式子来判断交点是否在三角形内,如果交点在三角形内,那么 $\alpha, \beta, \gamma \ge 0$,并且 $\alpha + \beta + \gamma = 1$。
将两步合并,就得到了一种高效的算法:
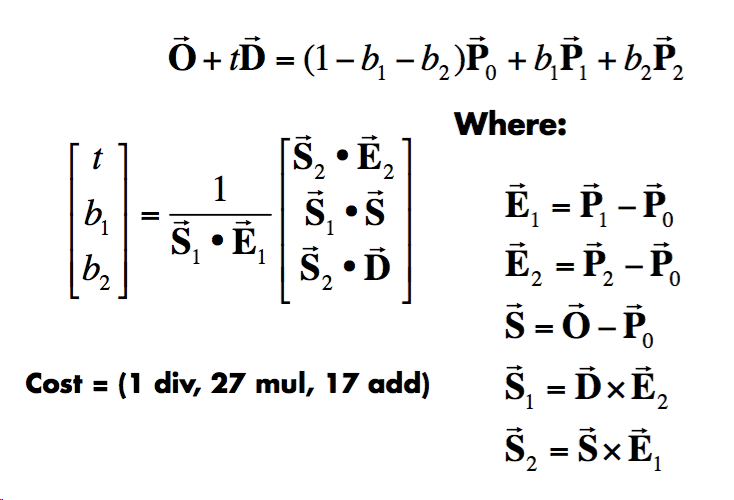
加速结构
必要性
通过上面的讨论,我们可以得到一种暴力的光线追踪算法:对于每一条发出的光线,与所有三角形求交,选择 t 最小的作为最近的交点。
即使每个像素只发出一条光线,时间复杂度也有像素数、反射次数和三角形数的乘积。在实际应用中,像素数和三角形数都非常多,因此这种算法的效率非常低。
包围盒

为了提高效率,我们可以使用包围盒(Bounding Box)来优化。顾名思义,包围盒将物体(或其一部分)的所有三角形包围在内,这样就可以快速判断光线是否与物体相交。如果光线没有与包围盒相交,那么肯定也不会与物体相交;如果光线与包围盒相交,再对三角形求交。
为了达到加速效果,包围盒与光线求交一定要尽量简单,采用比较广泛的是轴对齐包围盒(Axis-Aligned Bounding Box,AABB)。AABB 是一个立方体,而且每个面都与坐标轴平行。因此 AABB 需要 6 个参数来描述,例如 $x$, $y$, $z$ 的范围。
为了推导 AABB 与光线相交的算法,我们不妨将 AABB 看作三对「平行板」围成的体积。而光线要与之相交,必须存在一个时刻的点同时位于三对平行板的内部。而且这可以分开处理,如下图所示的二维情形:
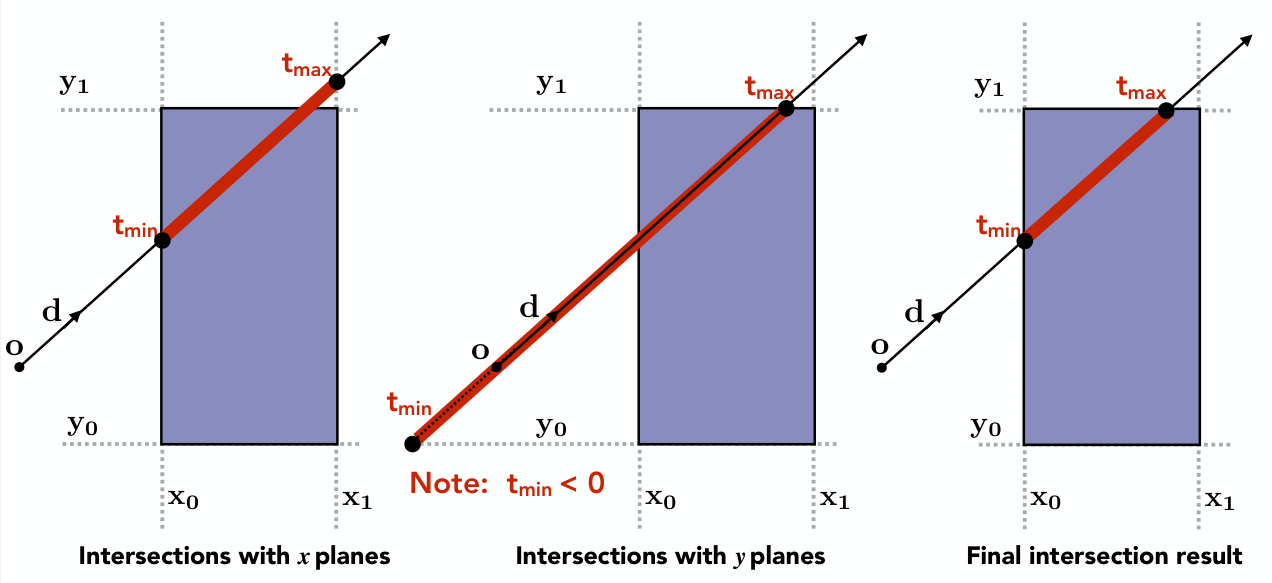
推广到三维,对三个 t 范围联立,只要保证进入时间 $t_{in}$ 小于离开时间 $t_{out}$,就可以判断光线与 AABB 相交。当然,由于射线的方向性,还需要判断 $t_{out}$ 是否大于 0。
AABB 还可以用于碰撞检测,其原理与光线追踪类似。
均匀网格
将空间均匀分成三维网格,每个格子就是一个包围盒,包围盒中保存了所有与其相交的三角形(三角形可能跨网格)。这样,对于每条光线,只需要与「沿途」的网格中的三角形求交,就可以得到最近的交点。
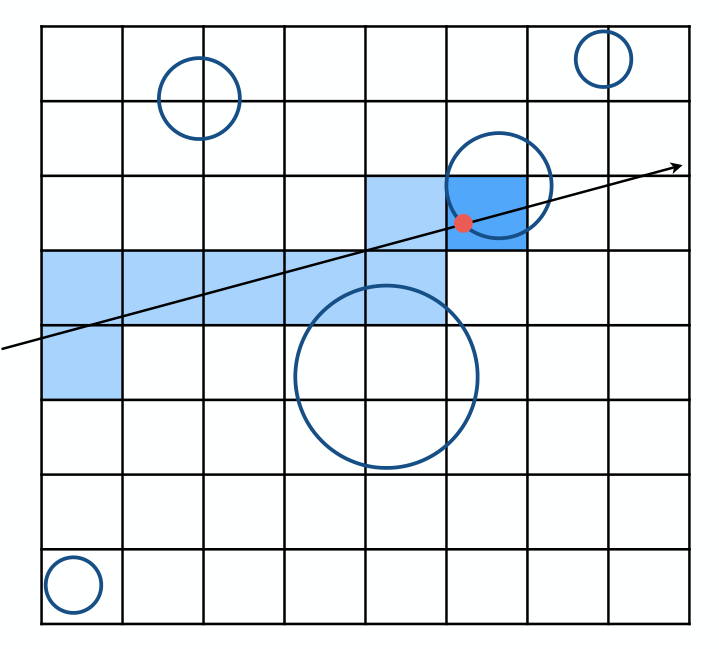
怎么确定「沿途」的网格呢?实际上,这和光栅化直线很类似。例如在上图中,光线的「斜率」在第一象限,因此下一个格子不是在右边就是在上面,if 一下就能找到。实际上有更加巧妙的画线算法,例如 Bresenham 算法,不需要分支就能快速计算出下一个格子。这里不再赘述,感兴趣的读者可以自行查阅。(GAMES101 似乎不讲,但是我校的 CG 课程有所展开,大概因为这些内容不太「现代」)
均匀网格实现很简单,但是网格大小是固定的,但是场景中物体的分布一般不均匀,因此会造成很多空网格和密集网格。这样就会造成很多不必要的计算。实际应用中,基本不会用均匀网格。
基于空间的分割
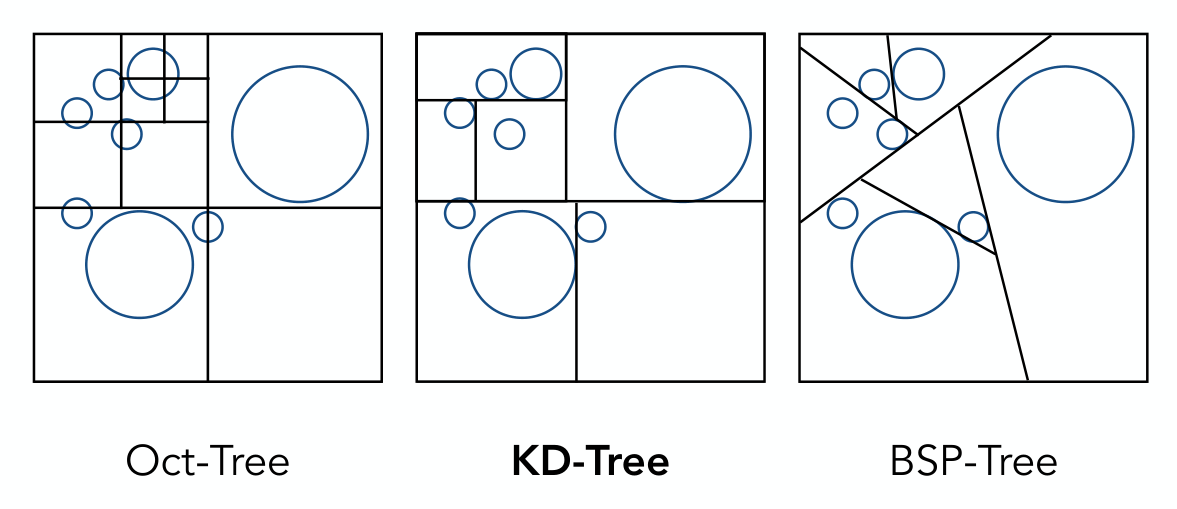
既然均匀分割不太好,那么我们可以根据物体的分布来分割空间。这样的方法包括八叉树、KD 树、BSP 树等。这些方法都是每次将空间分成两部分,最终形成树状结构。
注意一个三角形可能会跨越多个区域,因此要尽量减少切割面分割三角形,否则最终会产生远多于初始的三角形数量(如果切割面斜着分割三角形,会产生一个三角形和一个四边形,相当于三个三角形),降低效率。三角形保存在叶节点。
另一个问题是如何确定分割的规则,这还是比较困难的。对于没有物体的区域,显然可以停止分割;但对于有物体的区域,分割到什么程度才算合适,没有一个明确的标准。八叉树、KD 树和 BSP 树对每次分割的规则不同,八叉树要求最严格,BSP 树要求最宽松,而 KD 树则介于两者之间。
以 KD 树为例,每次分割都与坐标轴平行。下图展示了使用 KD 树加速光线追踪的过程:
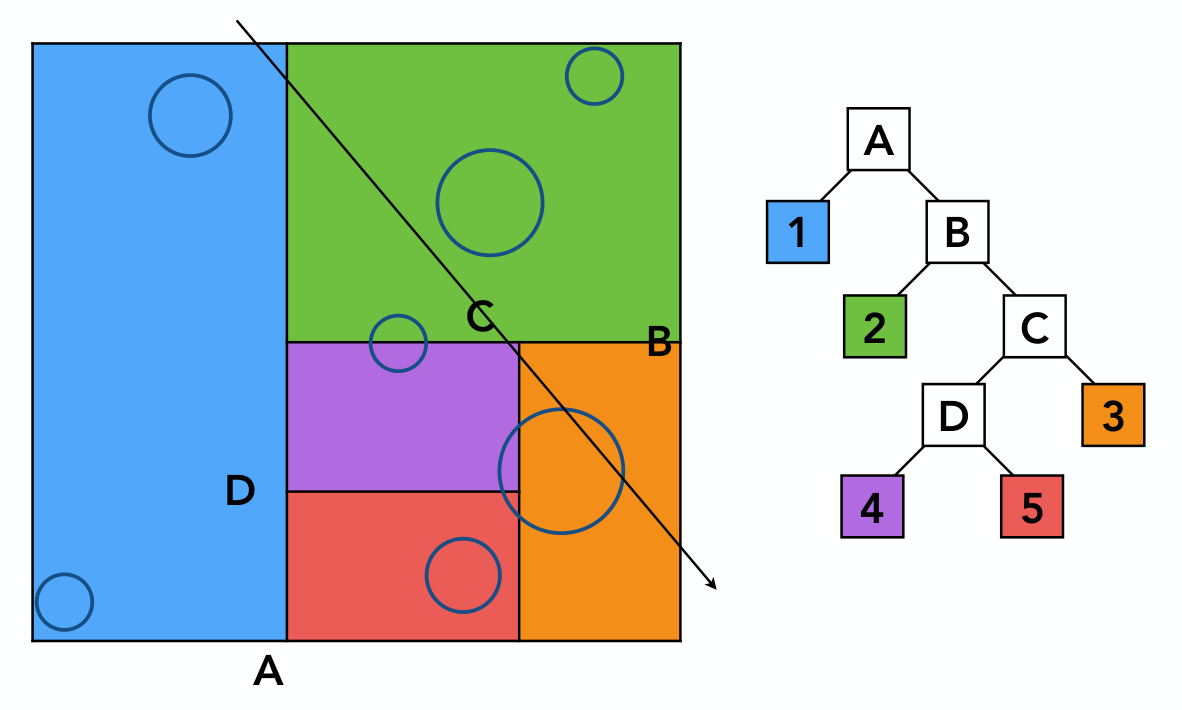
对于光线途径的每个叶节点,都需要与其中的三角形求交。在图中的例子中加速效果看起来不明显,但当树的深度较大时,加速效果就很明显了。
BVH
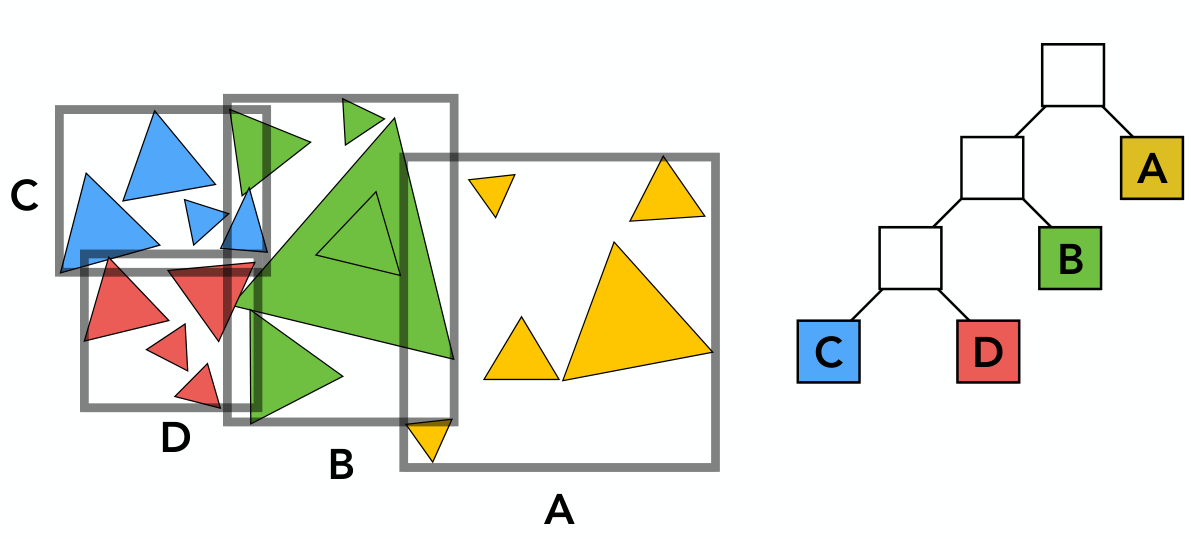
与上述基于空间的分割不同,BVH 是基于物体的分割。BVH 的全称是 Bounding Volume Hierarchy,即包围盒层次。在构建 BVH 树的过程中,每次将物体分成两部分,并重新计算包围盒,最终形成树状结构。
注意现在一部分空间可能属于多个包围盒,也就是说,包围盒之间可能有交集。三角形还是保存在叶节点。
BVH 的分割规则也没有定论,可以采用的启发式规则包括选择最长的轴分割,每次分割两边的物体数量接近,当物体很少时不再分割等。
BVH 的遍历和上面类似,不再赘述。下图总结了基于空间和基于物体的分割的区别:
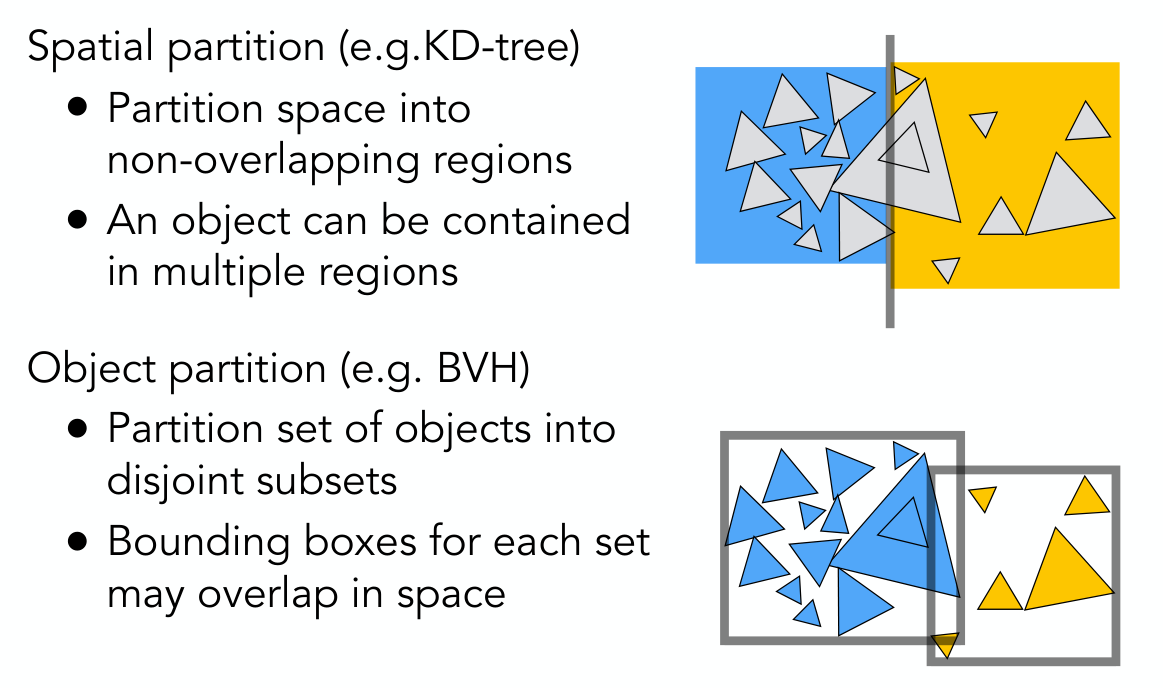
此外,在我校 CG 进阶课程,讲 BVH 优化的课上(因为 CPC 去看的),介绍了高级的 BVH 构建方法。

基于包围盒面积的命中概率估计来选择最优的分割点。尽可能最小化分割后包围盒的面积和,这样可以减少遍历的节点数量。
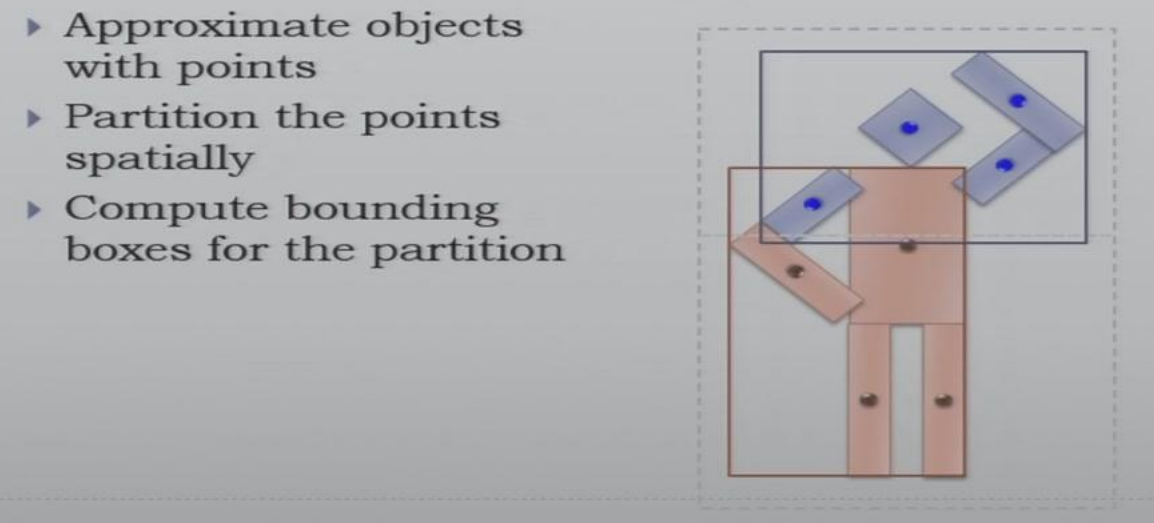
将基本形状视为点来完成分割。

使用贪心算法,认为每次选择最优的分割点,最终得到的树是接近最优的。
从下面的内容开始,就不是传统 CG 课程的内容啦!
实时光线追踪*
可先行阅读 https://www.anandtech.com/show/13282/nvidia-turing-architecture-deep-dive
* anandtech 是一个非常好的网站,保存了从 1997 年成立以来各种 CPU、GPU 和其他 PC 硬件的评测文章,非常适合考古。
P.S. Tom’s Hardware 成立时间也类似,也能找到很好的早年评测文章

我看了一圈,感觉和 Tensor Core / DLSS 比起来,RT Core 的资料实在是太少了。NVIDIA 给出的官方资料就不多,而且这类 ASIC 设计似乎也不是很吸引人。而且似乎还是 RTX 20 系发布时报道多一点,大概是后来大家都无所谓了。因此接下来基本上简单总结一下 anandtech 的文章内容。
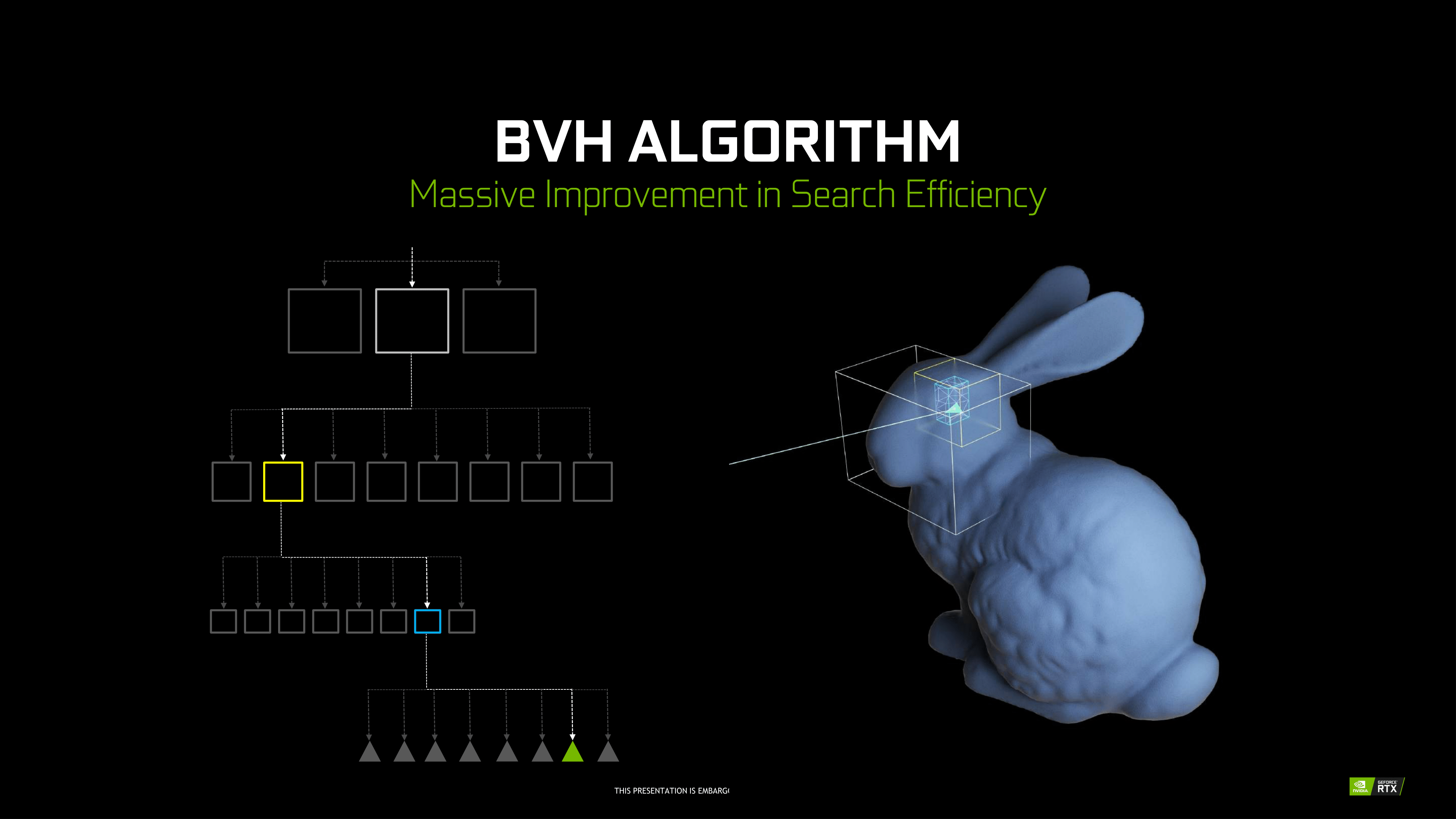
BVH 是目前光线追踪的主流,实时光线追踪用的也是 BVH,只不过 BVH 的构建和遍历都是在 GPU 上完成的。上图更加生动的展示了 BVH 的结构。
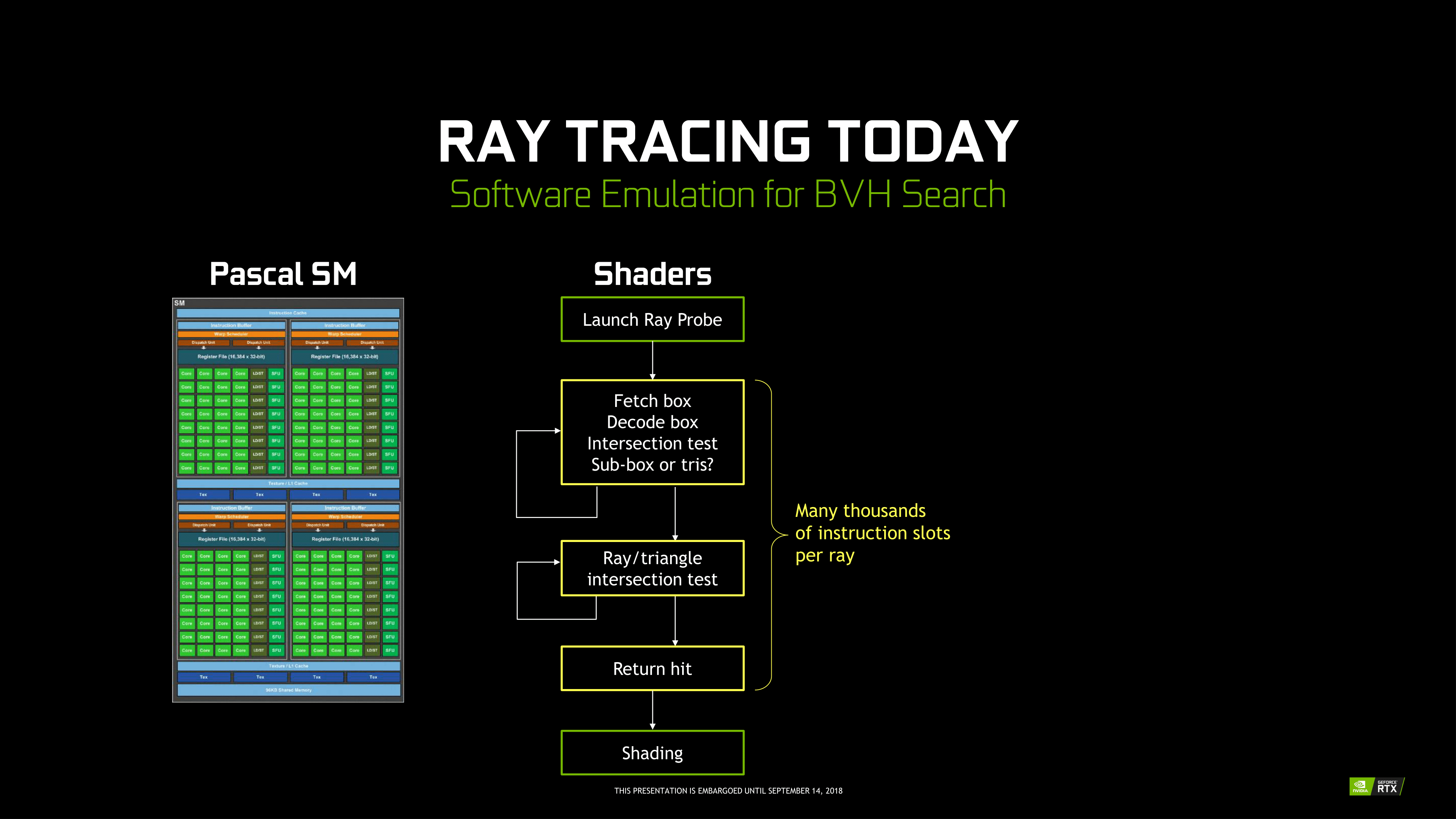
传统上,用 GPU 的可编程 shader 来软件模拟光线追踪,其效率可能高于 CPU,但可能难以到达实时的水平。追踪每条光线可能需要上千条指令来完成。因此硬件加速就显得很有必要,尤其是认为光线追踪是未来主流的 NVIDIA。
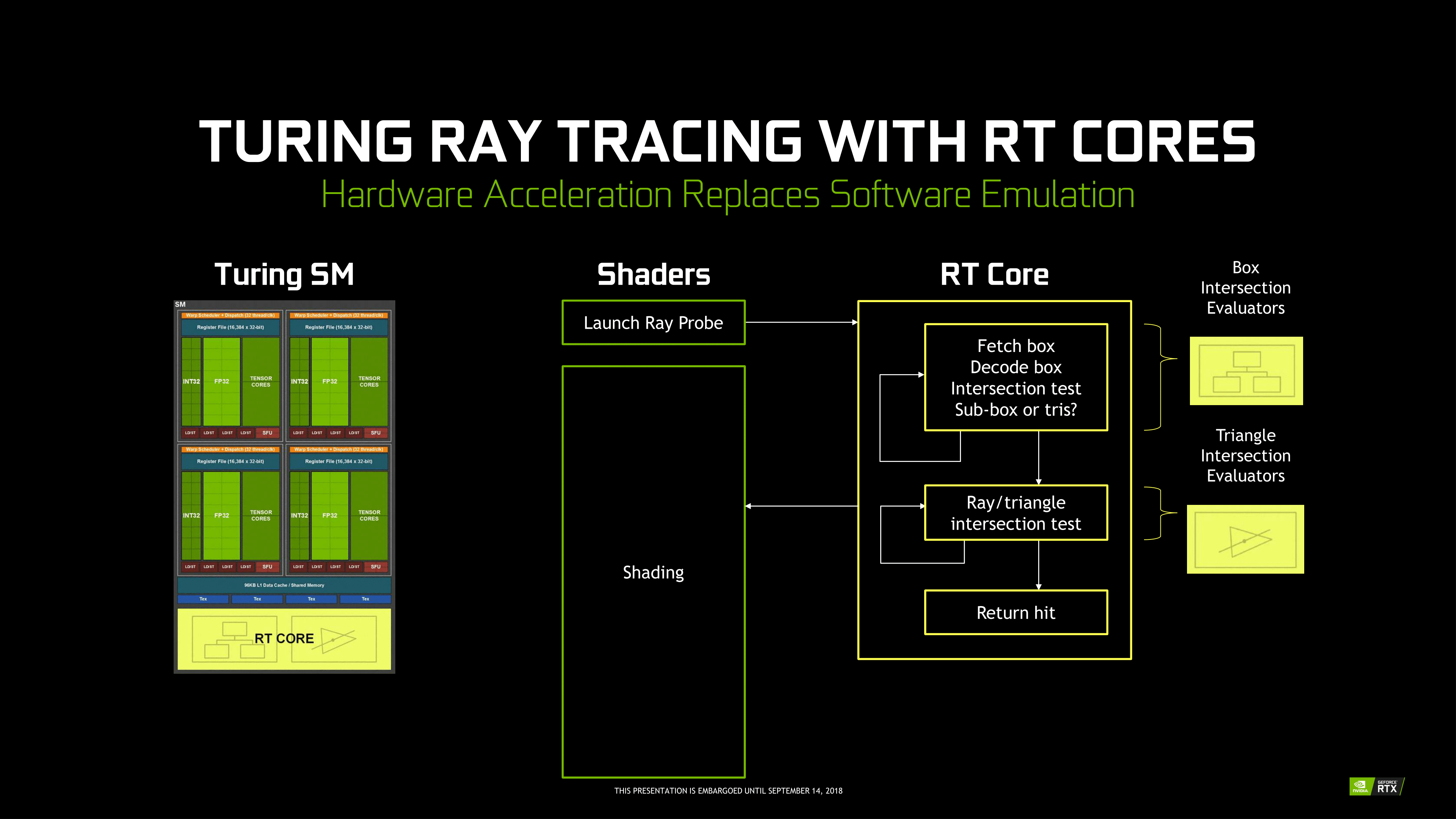
因此,RT Core 就是把计算量最大的部分,即光线遍历和求交的计算,放到了特殊的硬件上。不过,光线追踪的空间局部性并不好,对于内存带宽是一个挑战。
路径追踪*
我暂时放弃了,看到 Rendering Equation 感觉就很假了(
可以看 https://www.youtube.com/watch?v=gsZiJeaMO48 直观感受一下。
