前言
由于上个月只写了理论部分,这个月加上一些简单实现与优化。
主要希望简单过一遍 Ray Tracing in One Weekend 和后续系列(optional),另外还有著名的 smallpt: Global Illumination in 99 lines of C++。
至于优化部分主要是「汇编与接口」课程的项目,因此以 SIMD 为主(项目 12 月底截止)
输出图像
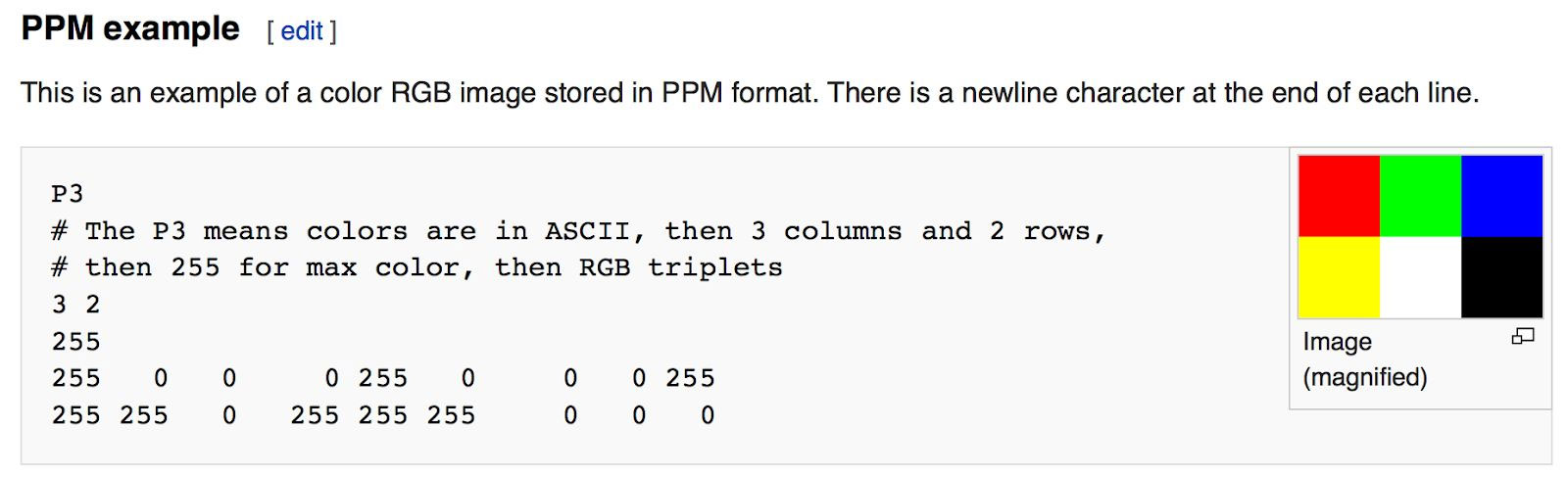
PPM 格式确实非常好,可以做到人类可读(P3),最早应该是为了 ASCII 邮件发送设计的。也可以用二进制保存(P6),但都没有压缩。我们 CG 课程作业一开始也是用 PPM 的,后来载入纹理我也没改代码继续用 PPM。优点是不需要额外的库,十几行代码就能实现。缺点是文件大。
P6 与 P3 头部格式一样,但位图数据直接用二进制保存。
在 Windows 下可以找 Netpbm 的 Windows 版本,不过我用的是 GIMP。
代码
复用了 CG 作业的代码:
1
2
3
4
5
6
7
8
9
10
| void ppmWrite(const char *filename, uint8_t *data, int w, int h)
{
FILE *fp;
fp = fopen(filename, "wb");
fprintf(fp, "P6\n%d %d\n255\n", w, h);
fwrite(data, w * h * 3, 1, fp);
fclose(fp);
}
|
主程序如下,对书中代码做了魔改:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| int main()
{
const int image_width = 256;
const int image_height = 256;
uint8_t data[image_width * image_height * 3];
for (int i = 0; i < image_height; i++)
{
cerr << "\rScanlines remaining: " << image_height - i << ' ' << flush;
for (int j = 0; j < image_width; j++)
{
int base = (i * image_width + j) * 3;
float r = 1.0 * i / (image_height - 1);
float g = 1.0 * (image_width - j - 1) / (image_width - 1);
float b = 0.25;
data[base + 0] = (uint8_t)(255.999 * r);
data[base + 1] = (uint8_t)(255.999 * g);
data[base + 2] = (uint8_t)(255.999 * b);
}
}
ppmWrite("image.ppm", data, image_width, image_height);
cerr << "\nDone. " << endl;
return 0;
}
|

与书中结果一致。但显然输出非常快,进度条没有起到作用(
vec3 类
书中不使用齐次坐标,因此只需要 vec3 即可表示点和向量。vec3 实在是太简单了,直接交给 Copilot 生成:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| struct vec3
{
float x, y, z;
vec3() : x(0), y(0), z(0) {}
vec3(float x, float y, float z) : x(x), y(y), z(z) {}
vec3 operator+(const vec3 &v) const { return vec3(x + v.x, y + v.y, z + v.z); }
vec3 operator-(const vec3 &v) const { return vec3(x - v.x, y - v.y, z - v.z); }
vec3 operator*(float f) const { return vec3(x * f, y * f, z * f); }
vec3 operator/(float f) const { return vec3(x / f, y / f, z / f); }
vec3 operator-() const { return vec3(-x, -y, -z); }
float dot(const vec3 &v) const { return x * v.x + y * v.y + z * v.z; }
vec3 cross(const vec3 &v) const { return vec3(y * v.z - z * v.y, z * v.x - x * v.z, x * v.y - y * v.x); }
float length() const { return sqrt(x * x + y * y + z * z); }
vec3 normalize() const { return *this / length(); }
vec3 &operator+=(const vec3 &v)
{
x += v.x;
y += v.y;
z += v.z;
return *this;
}
vec3 &operator-=(const vec3 &v)
{
x -= v.x;
y -= v.y;
z -= v.z;
return *this;
}
vec3 &operator*=(float f)
{
x *= f;
y *= f;
z *= f;
return *this;
}
vec3 &operator/=(float f)
{
x /= f;
y /= f;
z /= f;
return *this;
}
};
vec3 operator*(float f, const vec3 &v) { return v * f; }
float dot(const vec3 &v1, const vec3 &v2) { return v1.dot(v2); }
vec3 cross(const vec3 &v1, const vec3 &v2) { return v1.cross(v2); }
float length(const vec3 &v) { return v.length(); }
vec3 normalize(const vec3 &v) { return v.normalize(); }
ostream &operator<<(ostream &os, const vec3 &v)
{
os << v.x << ' ' << v.y << ' ' << v.z;
return os;
}
void write_color(uint8_t *pixel_start, const vec3 &color)
{
pixel_start[0] = (uint8_t)(255.999f * color.x);
pixel_start[1] = (uint8_t)(255.999f * color.y);
pixel_start[2] = (uint8_t)(255.999f * color.z);
}
|
看起来有很多用不上的,但反正都是自动生成的,就不删了。接下来改主程序,不再赘述。
光线,简单相机和背景
光线
光线的表示非常简单,正如前面理论部分所说,由原点和方向表示。
1
2
3
4
5
6
7
8
| struct ray
{
vec3 orig;
vec3 dir;
ray() {}
ray(const vec3 &orig, const vec3 &dir) : orig(orig), dir(dir) {}
vec3 at(float t) const { return orig + t * dir; }
};
|
相机
接下来是书中给出的坐标系、相机定义,最好直接用,这样后面的代码就不用改了。不过其实有个小问题,下图的宽高比是 2:1,而代码中实际用的是 16:9,需要读者注意一下。
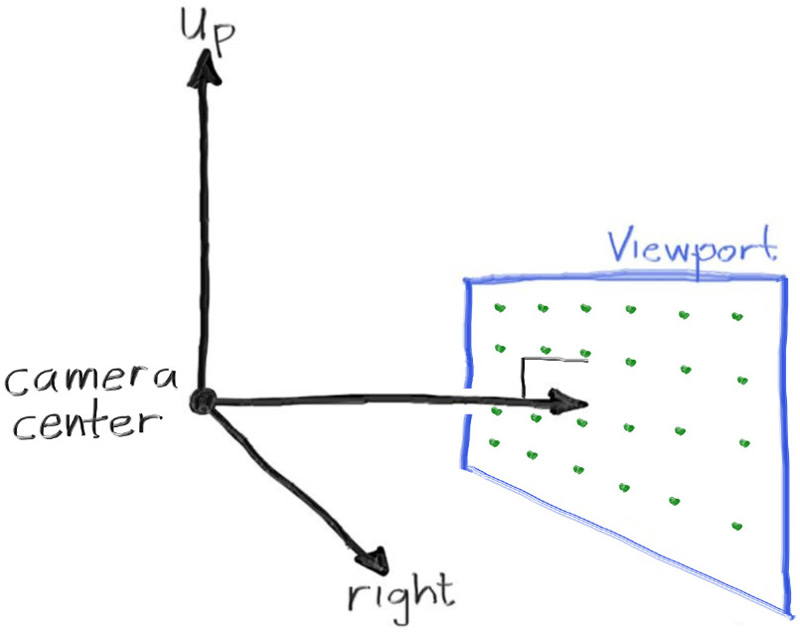
作者手绘的,是不是很不错?
背景
然后是用 ray 线性插值计算背景颜色的函数,可以说是强行用 ray 类了:
1
2
3
4
5
6
| vec3 color(const ray &r)
{
vec3 unit_direction = normalize(r.dir);
float t = 0.5f * (unit_direction.y + 1.0f);
return (1.0f - t) * vec3(1.0f, 1.0f, 1.0f) + t * vec3(0.5f, 0.7f, 1.0f);
}
|
首先将 Y 范围从 [-1, 1] 映射到 [0, 1],然后用线性插值计算颜色,两端分别是白色和天蓝色。
接下来就是主程序,每个像素计算了 u, v 坐标(纹理?),然后用这个坐标构造了一条光线。常量就看书吧。
1
2
3
4
5
6
7
8
9
10
11
12
| for (int i = 0; i < image_height; i++)
{
cerr << "\rScanlines remaining: " << image_height - i << ' ' << flush;
for (int j = 0; j < image_width; j++)
{
int base = (i * image_width + j) * 3;
float v = 1.0f * (image_height - i - 1) / (image_height - 1);
float u = 1.0f * j / (image_width - 1);
ray r(origin, lower_left_corner + u * horizontal + v * vertical - origin);
write_color(data + base, color(r));
}
}
|

插曲:精度之争
值得一提的是,你可能注意到我用的都是 float 而不是 double,因为在一般 CG 中,float 的精度已经足够了,而且速度更快。而且在一般的 GPU 上,单精度比双精度算力高很多,在 CPU SIMD 中也有 2 倍的吞吐量。不过,如果不用 GPU 或 SIMD,那么速度差别就不大了。
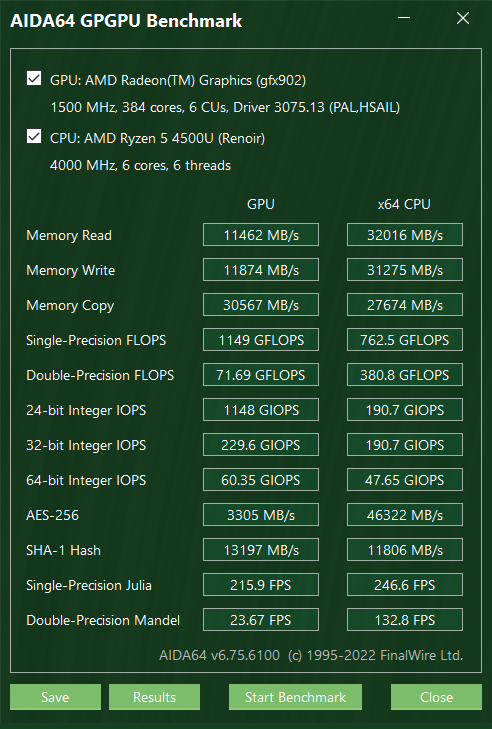
以下是使用 AIDA64 GPGPU Benchmark 测试的结果,反映的都是峰值性能。首先是我的笔记本:
这是计网实验室的台式机:
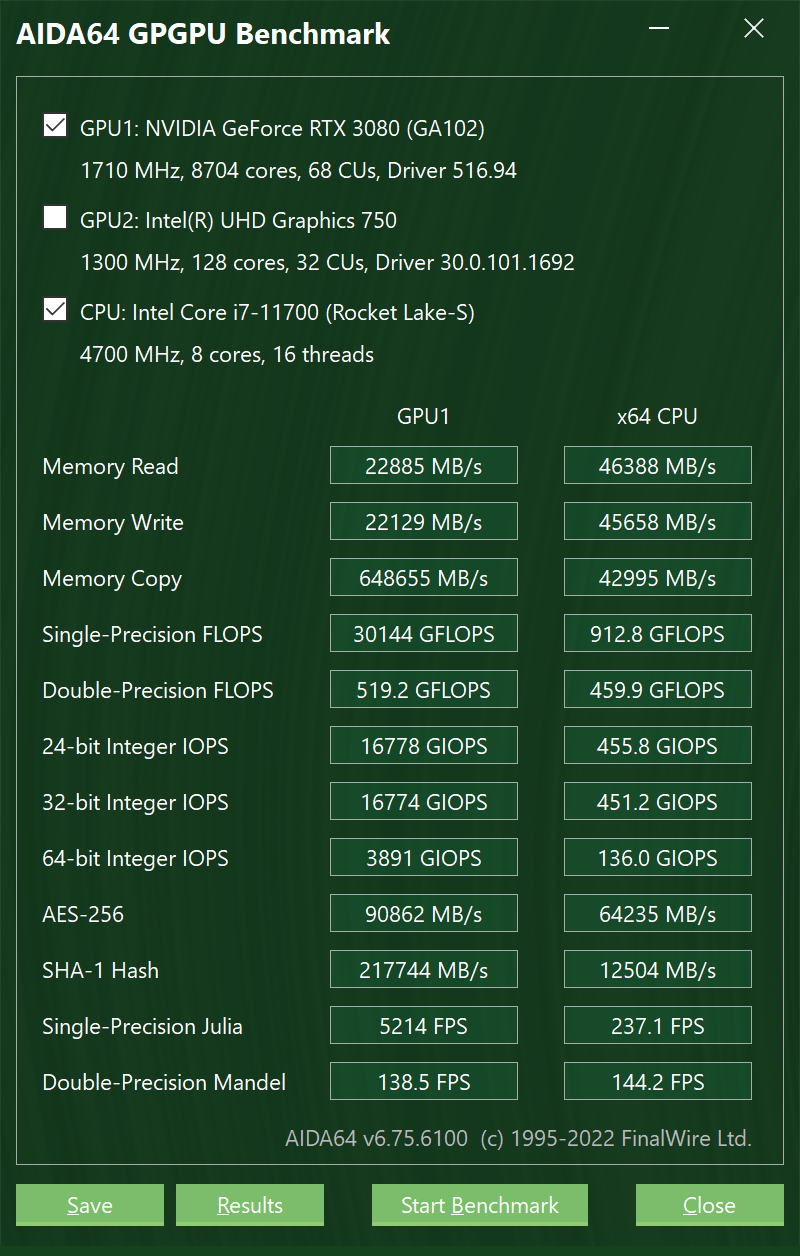
快去计网实验室玩游戏炼丹挖矿吧!
球体
回忆一下,在理论部分,我们定义光线方程为
$$\mathbf{r}(t) = \mathbf{o} + t \mathbf{d}$$
其中 $\mathbf{o}$ 是原点,$\mathbf{d}$ 是方向,$t$ 是参数。
定义球体方程为
$$(\mathbf{p} - \mathbf{c}) \cdot (\mathbf{p} - \mathbf{c}) = r^2$$





